About Logistic Model

Logistic model was developed by Belgian mathematician Pierre Verhulst (1838) who suggested that the rate of population increase may be limited, i.e., it may depend on population density :

Z_n+1 = r Z_n (1 - Z_n) ,

where r is the Rate and Z_n is the concentration of n^th year.

It is said that, this equation governs almost all the density (population, growth, etc.) in the universe. The curve generated on basis of the input parameters have some certain variations.

Important Features :

Logistic Map Behavior Dependency on 'r' :

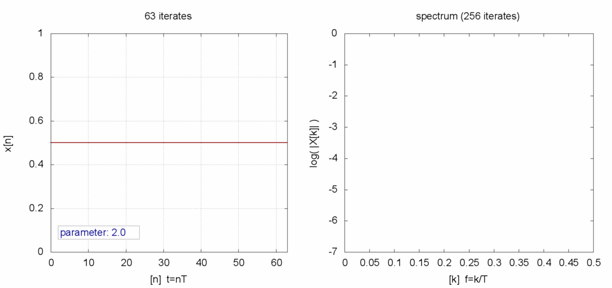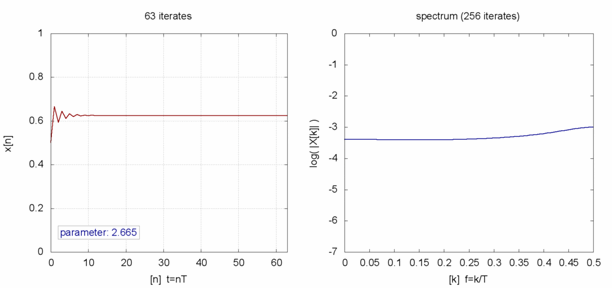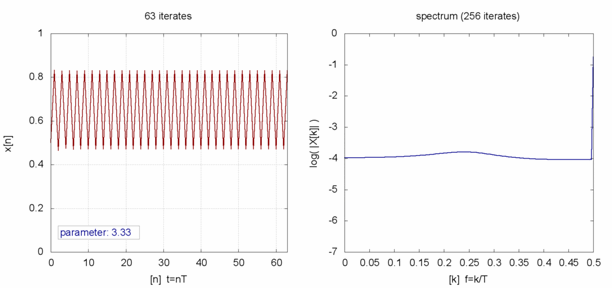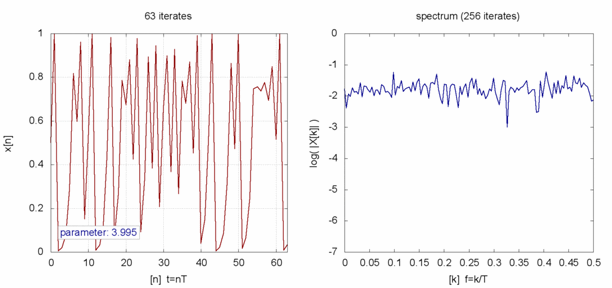
Amplitude and frequency content of some logistic map iterates for parameter values ranging from 2 to 4

With $r$ between 0 and 1, the population will eventually die, independent of the initial population.
With $r$ between 1 and 2, the population will quickly approach the value $r - 1 / r$ , independent of the initial population.
With $r$ between 2 and 3, the population will also eventually approach the same value $r - 1 / r$ , but first will fluctuate around that value for some time.
With $r$ between 3 and 1 + √6 ≈ 3.44949, from almost all initial conditions the population will approach permanent oscillations between two values. These two values are dependent on $r$ .
With $r$ between 3.44949 and 3.54409 (approximately), from almost all initial conditions the population will approach permanent oscillations among four values.
With $r$ increasing beyond 3.54409, from almost all initial conditions the population will approach oscillations among 8 values, then 16, 32, etc. The lengths of the parameter intervals that yield oscillations of a given length decrease rapidly; the ratio between the lengths of two successive bifurcation intervals approaches the Feigenbaum constant $δ \approx 4.66920$ . This behavior is an example of a period-doubling cascade.
At $r \approx 3.56995$ is the onset of chaos, at the end of the period-doubling cascade. From almost all initial conditions, we no longer see oscillations of finite period. Slight variations in the initial population yield dramatically different results over time, a prime characteristic of chaos.
Beyond $r = 4$ , almost all initial values eventually leave the interval $[0,1]$ and diverge.

Bifurcation Diagram and CHAOS :

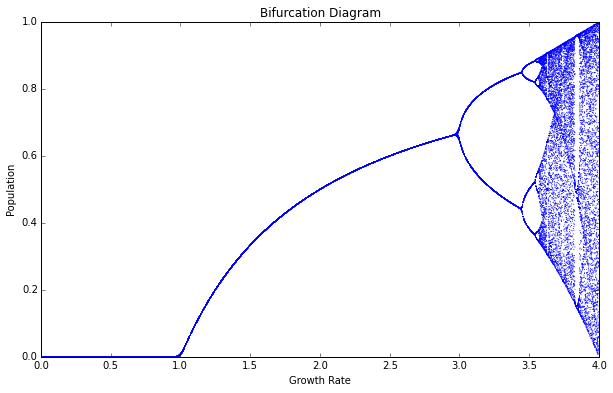
Bifurcation Diagram of Logistic Map

In mathematics, particularly in dynamical systems, a bifurcation diagram shows the values visited or approached asymptotically (fixed points, periodic orbits, or chaotic attractors) of a system as a function of a bifurcation parameter in the system.

We plot an Equilibrium Concentration or Population Vs Rate graph for rate < 4 that gives us the Bifurcation Diagram for the logistic map. For r > 3, we find that there are more than one equilibrium concentration and the number of such points double after a certain amount of change in r.

Here, bifurcations occur when there are more than one equilibrium points are found with respect to the rate (r).

The onset of CHAOS :

Beyond a growth rate of 3.6, however, the bifurcations ramp up until the system is capable of eventually landing on any population value. This is known as the period-doubling path to chaos. As you adjust the growth rate parameter upwards, the logistic map will oscillate between two then four then eight then 16 then 32 (and on and on) population values. These are periods, just like the period of a pendulum.

By the time we reach growth rate 3.9, it has bifurcated so many times that the system now jumps, seemingly randomly, between all population values. I only say seemingly randomly because it is definitely not random. Rather, this model follows very simple deterministic rules yet produces apparent randomness. This is chaos: deterministic and aperiodic.

About the Project :

I made this project to visualize and show the beauty of this simple equation which fascinated me from the very first day I got to know this.